Reference textbooks are unfortunately not infallible! This web page lists some of the textbook errors that have been discovered by mathStatica. The examples below show that even the most highly respected statistics reference texts contain serious errors, and so illustrates the importance of checking all of one's work with a computer.

We would like to stress that the purpose of this page is not to find fault with these books. Quite the opposite, these texts have been selected for inclusion here because they are superb reference texts. Nor is it our intention to suggest that computers are flawless. But, computer software such as mathStatica does have the advantage that it makes it relatively easy to check one's work using different methods, which one should always take the trouble to do.

If you discover a textbook error by using mathStatica, please feel welcome to send it to us. After suitable checking, we would be happy to include it on this page (with attribution).

Textbook Errors

 Plotting the Pearson System

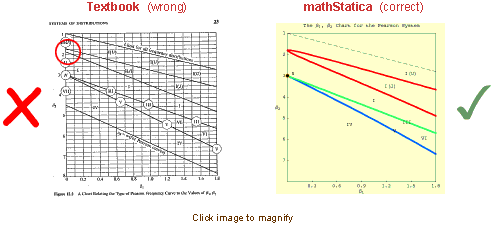
The diagram on the left is the reference textbook diagram of the Pearson system, as shown in Johnson, Kotz and Balakrishnan (1994, p.23) and Ord (1972, p.10); this diagram is actually incorrect. The correct diagram is shown on the right as obtained using mathStatica's interactive PearsonPlot function.

Textbook Error
Let random variable X have a Laplace distribution. Johnson, Kotz and Balakrishnan (1995, p.168) give the pdf of the r ^th order statistic as:

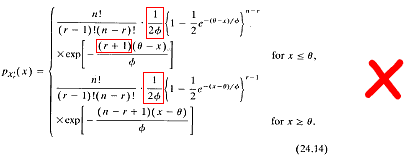
Unfortunately, this solution is incorrect.
 

mathStatica Solution
To obtain the correct solution, we first enter the pdf of our Laplace random variable into the computer:

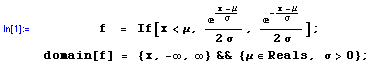
Then, the pdf of the r ^th order statistic is given by mathStatica as:

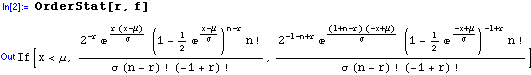
It can also be shown that the subsequent equations in Johnson, Kotz and Balakrishnan (1995), namely (24.15), (24.17) and (24.18) are all incorrectly deflated by a factor of two.

  Pareto Distribution: Joint Order Statistics

Textbook Error
Let random variable X have a Pareto(a, k) distribution. Johnson, Kotz and Balakrishnan (1994, p.599) give the joint pdf of the r ^th and s ^th order statistics, for r < s, as:

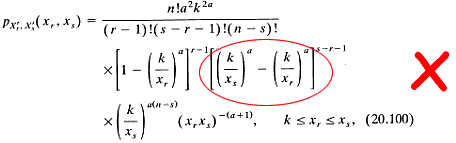
This can yield negative values!
 

mathStatica Solution

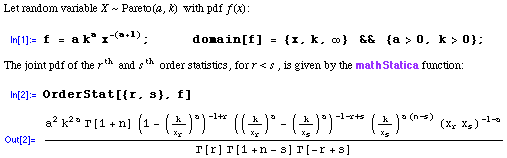
  Chi-squared Distribution: The Mean Deviation

Textbook Error
Johnson, Kotz and Balakrishnan (1994, p.420) give the mean deviation of a chi-squared random variable as:

mathStatica Solution
With mathStatica, it is easy to show that the circled '1' should be a '2', as shown in Rose and Smith (2002, p.422).

  Moments of Moments: Product cumulants

Textbook Error
In 1928, Fisher published the product cumulants of the k-statistics, which are now listed in reference bibles such as Stuart and Ord (1994). Here is the solution to 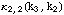as derived by Fisher in 1928 and listed in Stuart and Ord (1994, equation 12.70):

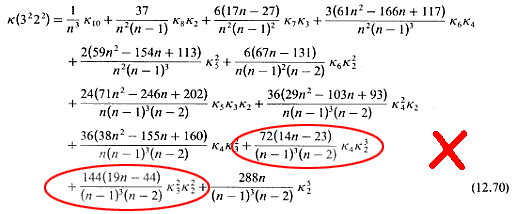
Unfortunately, this known textbook 'solution' is still incorrect after more than 70 years [Rose and Smith (2002, pp. 269-271) provide a proof].
 

mathStatica Solution
Here is the correct solution as derived by mathStatica:
(the second and third terms of the output correct the old mistake)

There is also a small typographic error in Stuart and Ord equation 12.66:

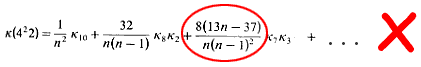
which should correctly be 8(13n - 17) rather than 8(13n - 37).

  Bivariate Half-Normal Distribution: Regression Function

Textbook Error
Kotz, Balakrishnan and Johnson (2000, p.327) consider the bivariate half-Normal distribution whose marginal distributions are both half-Normal. They provide the pdf and the regression function:

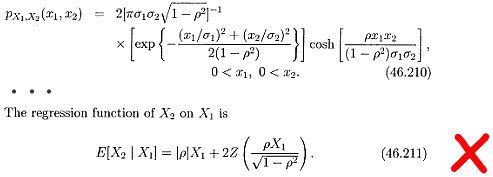
where Z(.) denotes the pdf of a N(0,1) random variable. Unfortunately, this solution is wrong.
 

mathStatica Solution
To obtain the correct solution, we start by entering the joint pdf into the computer:

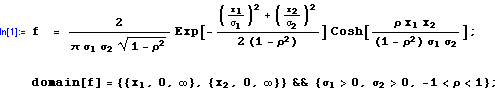
Then, the regression function can be derived in two steps with mathStatica:

(i) Derive the conditional pdf of X₂ given X₁ = x₁:

with domain of support:

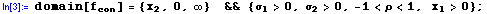
(ii) Derive the regression function :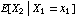

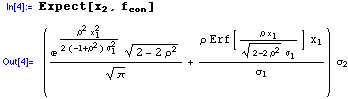
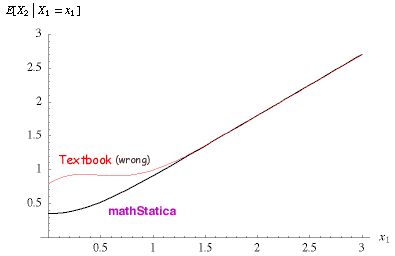
Ta dah! The following diagram compares the incorrect textbook solution (KBJ 2000) with the mathStatica solution, when the variances are 1 and :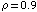

  Johnson Family: Third Central Moment

Textbook Error
Stuart and Ord (1994, Section 6.35) give the third central moment of Johnson's S_U   system as:

mathStatica Solution
Rose and Smith (2002, p.169) derive these moments using mathStatica. It appears a small typo has crept into Stuart and Ord and that the circled 'sin' function should be 'sinh'.

  Bivariate Exponential Distribution

Textbook Error
Spanos (1999, p.186) provides the following details on a Gumbel bivariate Exponential distribution:

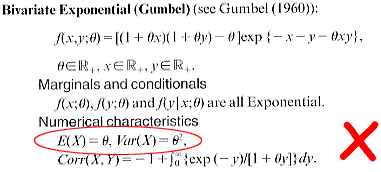
Unfortunately, the solutions in Spanos for the mean and variance are wrong.
 

mathStatica Solution
To obtain the correct solution, we start by entering the bivariate pdf into mathStatica:

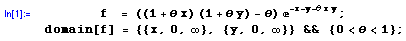
The correct mean and variance are then obtained as follows:

As an aside, we can also do a neater job deriving the correlation between X and Y:

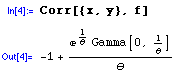
  Bivariate Uniform Distribution - à la Morgenstern

Textbook Error
Stuart and Ord (1994, p.267, Example 7.4) consider a bivariate Uniform distribution:

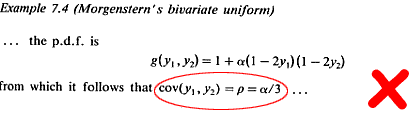
mathStatica Solution
To obtain the correct solution, we first enter the bivariate pdf into mathStatica:

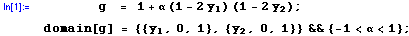
Then, derive Cov(Y₁ , Y₂ ):

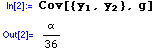
The correlation between Y₁ and Y₂ is:

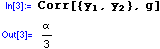
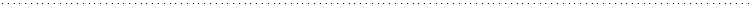
  Right-Censored Exponential Distribution: Mean

Textbook Error
Stuart and Ord (1994, p.214, Exercise 5.29) consider a right-censored Exponential distribution:

mathStatica Solution
We start by entering the Exponential pdf into mathStatica:

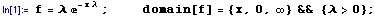
Let 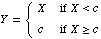denote an Exponential random variable right-censored at c.   We enter this into the computer as:

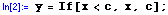
Then, the mean of a right-censored Exponential random variable is simply:

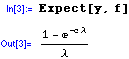
which is the correct answer.

  Multivariate Moments of Moments

Previously 'known' solution
Cook (1951) published results for many product cumulants of the bivariate k-statistics. Overall, Cook's paper in Biometrika is remarkably accurate. However, there is one error in the final part of Cook's solution to 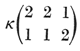, as published on pages 193 - 194 of Biometrika:

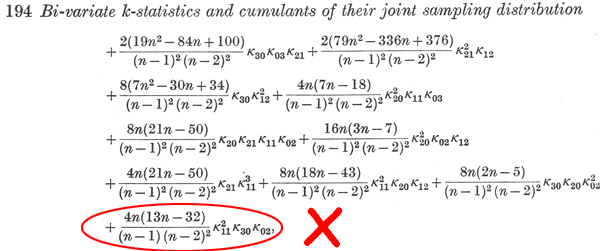
The final term is in error.
 

mathStatica Solution
Let  k21  denote the  KStatistic[{2,1}],   and  k12  denote  KStatistic[{1,2}] .

Then the correct solution is easily derived by mathStatica (v2 or later) as:

  Clayton copula

Textbook Error
Nelsen (2006, exercise 4.17) provides an algorithm that yields a Clayton copula. Unfortunately, this algorithm contains a small error (also in the first edition as exercise 4.15):

mathStatica Solution
We shall illustrate the error by solving the entire exercise, exactly as posed by Nelsen ...

Step 1: By independence, the joint pdf of X, Y and Z is f(x, y, z):

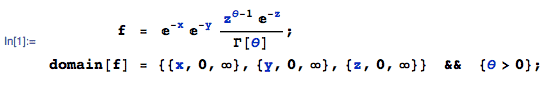
Step 2: The joint pdf of (U, V, W = Z) is:

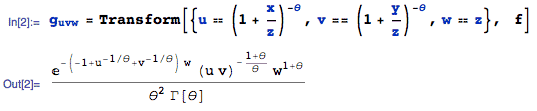
with domain of support:

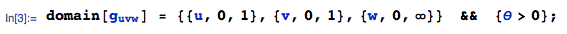
Step 3: We desire the marginal joint pdf of (U, V), which is:

with domain of support:

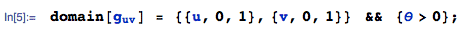
That’s it. Well, almost. The first paragraph of the exercise asks us to find the joint distribution function of (U, V).
i.e. find P(U < u, V < v):

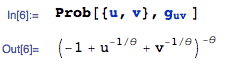
But ... this expression is not equal to the Clayton copula 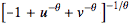. The green text above shows how to correct Nelsen’s exercise so that the method will work correctly.

  Shifted Exponential

Textbook Error   —   found by Prof Bruce McCullough
Devore and Berk (2012, Exercise Section 4.2: 19) consider a shifted Exponential model for traffic:

mathStatica Solution
Step 1: The pdf of X, say f(x), is:

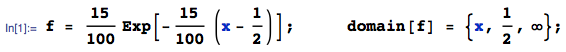
Part (a): The exact mean and standard deviation are:

... which are approximately 7.16 (not .15) and 6.66 (not .866) respectively.

Part (b): The probability that X is within one standard deviation of the mean is:

... which is approximately 0.864665 (not .9245).

Reference List

Cook, M. B. (1951)
    Bi-variate k-statistics and cumulants of their joint sampling distribution
    Biometrika, volume 38, 179-195

Devore, J. L. and Berk, K. N. (2012)
    Modern Mathematical Statistics with Applications, 2^nd edition, Springer

Fisher, R. A. (1928)
    Moments and product moments of sampling distributions
    Proceedings of the London Mathematical Society - series 2, volume 30, 199-238

Johnson, Kotz, Balakrishnan (1994)
    Continuous Univariate Distributions, volume 1, 2^nd edition

Johnson, Kotz, Balakrishnan (1995)
    Continuous Univariate Distributions, volume 2, 2^nd edition

Kotz, Balakrishnan, Johnson (2000)
    Continuous Multivariate Distributions, volume 1, 2^nd edition

Nelsen, R. B. (2006)
    An Introduction to Copulas, 2^nd edition (also 1^st edition)

Ord, J. K. (1972)
    Families of Frequency Distributions

Spanos, A. (1999)
    Probability Theory and Statistical Inference: Econometric Modeling with Observational Data

Stuart, A. and Ord, J. K. (1994)
    Kendall's Advanced Theory of Statistics - volume 1, 6^th edition