Order Statistics:     Non-identical distributions           New in mathStatica 2.0

Standard order statistic calculation assume that we are dealing with samples of independent and identically distributed (iid) variables. By contrast, mathStatica’s OrderStatNonIdentical function (new in mathStatica v2) generalises to independent non-identical distributions (cf. Rose and Smith, 2005). This is an enormously flexible and powerful capability.

Suppose we have three completely different distributions defined over three different domains of support … :
 
               f(x) is the pdf of a standard Exponential,
               g(x) is the pdf of a standard Cauchy, and
               h(x) is the pdf of a Uniform(-1, 1) random variable:

In[1]:=

Problem:    Consider a random sample of size n = 12. Of this sample, 5 values are drawn from the Exponential, 4 values are drawn from the Cauchy, and 3 from the Uniform. 
Find the pdf of the 2^nd smallest value from the sample, namely the second order statistic.

Solution:   The solution pdf, say φ(x), is simply:

In[2]:=

Out[2]=

with domain of support:      (we define piecewise functions over the real line)

In[3]:=

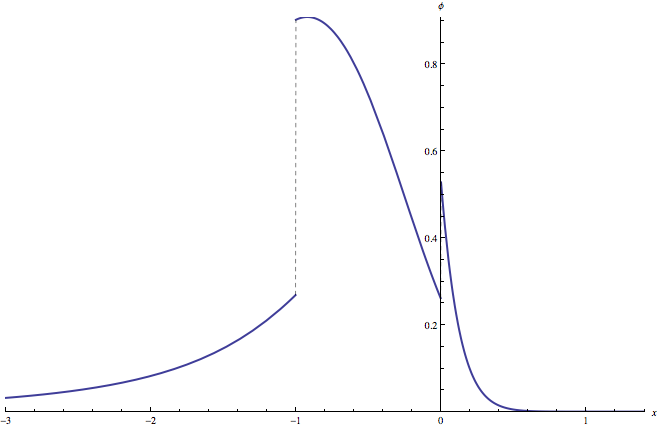
Here is a plot of the solution pdf:

In[4]:=

A quick Monte Carlo 'check’ of the exact solution we have just derived:
We want to generate, say, 200 000 pseudo-random samples, each of dimension 1×12. Each sample of 12 must consist of:   5 drawings from the Exponential(1), 4 drawings from the standard Cauchy, and 3 drawings from the Uniform(-1,1). An efficient way to proceed is to generate all 200 000 × 5  =  1 million pseudo-random Exponential drawings in one go, and all the 800 000 Cauchy drawings in one go etc., and then split the generated data into appropriate samples of size 12. This takes just 0.2 seconds to generate:

In[5]:=

Out[5]=

We now want to find, for each 1×12 sample, the second smallest value; i.e. the sample second order statistic. To do so, we Sort each sample, and then select the second element of the sorted sample using Part:

In[6]:=

We can now make a frequency plot to compare the pseudo-random Monte Carlo solution (—) with the theoretical symbolic solution φ(x) (—) derived above, using mathStatica’s FrequencyPlot function:

In[7]:=

Out[7]=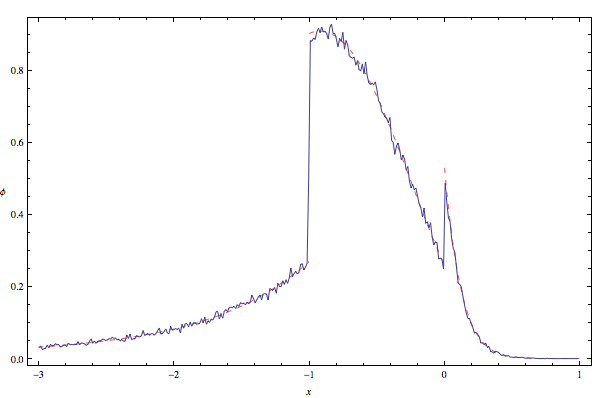

For the win!

References
Rose, C. and Smith, M. D. (2005), Computational order statistics, The Mathematica Journal, 9(4), 790–802.