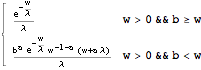Maximum of:       Triangular, Uniform and half-Halo           New in mathStatica 2.0

Consider three different distributions defined over three different domains of support …


Let     with pdf   f(x),   
    let     with pdf g(y), 
    and let Z ∼ half-Halo with pdf h(z):

In[1]:=

Here are the three pdf’s illustrated:

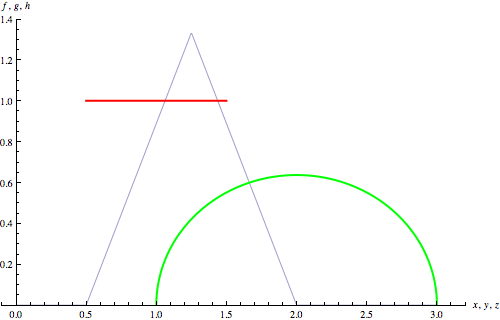
        Suprematism No. 1:    f(·) Triangular      g(·) Uniform        h(·) half-Halo

We seek the pdf of W = max(X, Y, Z) . The solution pdf is simply:

In[2]:=

Out[2]:=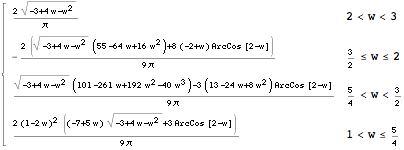

Here is a plot of the pdf of the maximum, together with the underlying pdf’s:

    Suprematism No. 2:  The Malevich Maximum —  pdf of the maximum, together with the 3 underlying pdf’s

Maximum of:       Six different Uniform random variables           New in mathStatica 2.0

Let with pdf f(x):

In[1]:=

Here are the six pdf’s corresponding to b = 1, 2, 3, 4, 5 and 6:

In[2]:=

Out[2]=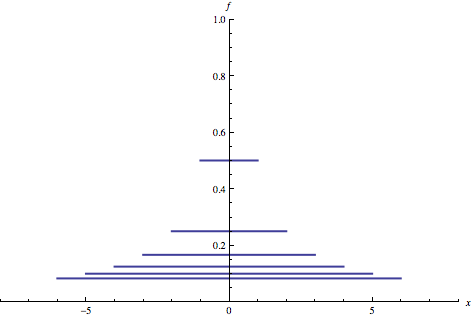

Problem: Find the pdf of .  

Solution: The solution pdf is simply:

In[3]:=

Out[3]=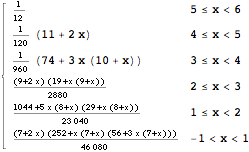

with domain of support:      (we define piecewise functions over the real line)

In[4]:=

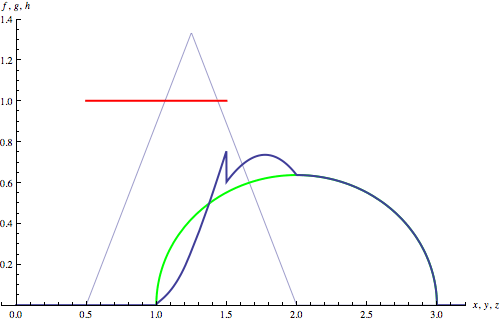
Here is a plot of the solution pdf:

In[5]:=

Out[5]=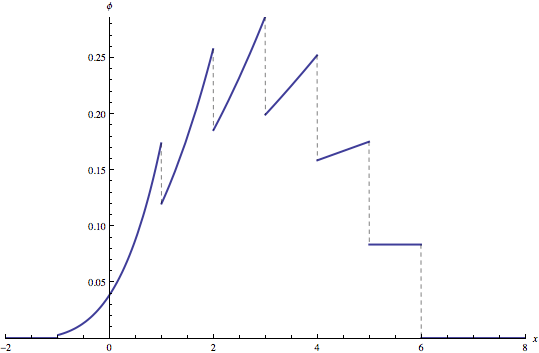

A quick Monte Carlo 'check’ of the exact solution we have just plotted:
We first generate 6 pseudo-random data sets corresponding to , and each containing 250000 pseudo-random drawings:

In[6]:=  

Next, we transpose from 6 data sets each of size 250000  … to … 250000 samples each of size 6. Each sample of 6 represents a single pseudo-random drawing from . Then, we map the Max function across each sample of 6, generating our 250000 empirical drawings of the sample maximum:

In[7]:=

We can now make a frequency plot to compare the pseudo-random Monte Carlo solution (—) with the theoretical symbolic solution φ(x) (—) derived above:

In[8]:=

Out[8]=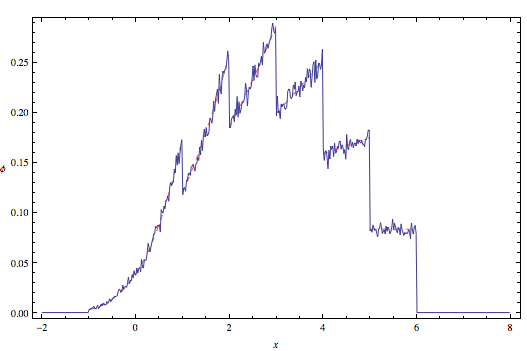

For the win!

Minimum of:       Pareto and Exponential           New in mathStatica 2.0

Let X ∼ Pareto(a, b)  with pdf f(x):

In[1]:=

and let Y ∼ Exponential(λ) with pdf g(y):

In[2]:=

Problem: Find the pdf of W = min(X, Y).

Solution: The solution is simply:

In[3]:=

Out[3]=