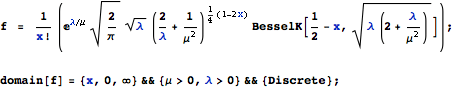
Let X be any discrete random variable with pmf f(x).
Here is the ugliest discrete distribution we could find: Holla’s distribution ... the pmf contains a BesselK function, it has no closed form cdf, it is non-invertible etc. So, to illustrate, let X ∼ Holla(μ, λ) with pmf f(x):
In[1]:= 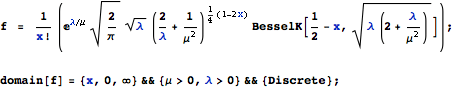
The DiscreteRNG function in mathStatica 2 takes less than ½ second to generate 1 million pseudo-random drawings from this beast:
In[2]:= ![]()
Out[2]= ![]()
Compare the EMPIRICAL distribution of data (▲) ]with the TRUE distribution of X (•):
In[3]:= ![]()
Out[3]= 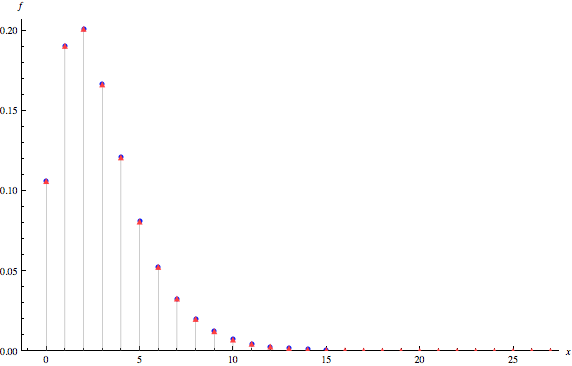
The triangular dots denote the empirical pmf, while the round dots denote the true density. One obtains a superb fit because mathStatica's DiscreteRNG function is an exact solution.
References
Rose, C. and Smith, M. D. (1997), Random number generation for discrete variables, Mathematica in Education and Research, Springer-Verlag, 6(3), 22–26.